01.07.2012 15:18

9.1. - Use tablas de verdad para establecer de las leyes del Morgan’s. 

 

Las tablas de verdad requeridas aparecen a continuación. Desde los valores en el examen final dos columnas son idénticas que las mesas verifican eso Del Morgan´s leyes sostenimiento.

p	q	p´	q´	p v q	p´ ^ q´	(p v q)´
0	0	1	1	0	1	1
0	1	1	0	1	0	0
1	0	0	1	1	0	0
1	1	0	0	1	0	0

 

p	q	p´	q´	p ^ q	p´v  q´	(p ^ q)´
0	0	1	1	0	1	1
0	1	1	0	0	1	1
1	0	0	1	0	1	1
1	1	0	0	1	0	0

 

9.2. - Con la ayuda de las leyes de álgebra del booleana verifique a lo siguiente:

(a) (p ˄ q´ ) ´ v r´= p´ v q v r´

(b)  ((p ˄ q´ ) ˄ (r  v (p ˄ q´ ))) ´ = p´v q

 

RESPUESTA:

(a)    (p ˄ q´ ) ´ v r´= p´ v q v r´  =  (p´ v q) v r´= p´ v q v r´  Usando De las leyes de Morgan´s, las leyes asociativas y (q´ ) ´= q.

(b)    ((p ˄ q´ ) ˄ (r  v (p ˄ q´ ))) ´ =

• =(p ˄ q´ ) v  (r  v (p ˄ q´ )) ´ por las leyes de Morgan´s
• =(p´ v q) v  (r´^ (p ˄ q´ )´ ) por las leyes de Morgan´s y el hecho que (q´ )´=q
• =(p´v q) v  (r´^(p´v q)) por las leyes de Morgan´s
• = ((p´v q) v r´ ) ^ (p´v q) por el distributivo y leyes de impotencia.
• = p´v q por la absorción y leyes de impotencia. 

 

 

9.3. - El hallazgo la forma normal disyuntiva del g = g (p, q, r, s) de función de Booleana) con la tabla de verdad mostrada en figura 9,19.

p	q	r	s	g
0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

 

RESPUESTA:

p´q´r´s   v  p´q´rs´  v  pq´rs  v pqr´s

 

 

 

9.4.- Estructura la tabla de verdad para la expresión  Booleana (p ^ (q ´ v r)) v (p´ ^ (q  v r´ )) y  determina su forma normal disyuntiva.

RESPUESTA:

Permita f = (p ^ (q´ v r)) v (p´ ^ (q v r´ )). La Tabla de verdad para f se da en figura s9.2

p	q	r	q´ v r	q v r´	p^(q´ v r)	p´^(q v r´ )	f
0	0	0	1	1	0	1	1
0	0	1	1	0	0	0	0
0	1	0	0	1	0	1	1
0	1	1	1	1	0	1	1
1	0	0	1	1	1	0	1
1	0	1	1	0	1	0	1
1	1	0	0	1	0	0	0
1	1	1	1	1	1	0	1

La forma normal disyuntiva es:

p´q´r´  v   p´qr´  v   p´qr  v  pq´r´  v   pq´r  v  pqr

 

 

 

9.5. - Escriba la expresión (p ^ el q´ ) ^ r 

(a) usando a sólo los operadores v y ´, 

(b) usando a sólo los operadores NAND. 

RESPUESTA:

(a) (p ^ q´ ) ^ r = (((p ^ q´ ) ^ r) ´ ) ´= ((p ^ q´ ) ´ v r´ ) = ((p´v q) v r´ ) ´= (p´v q v r´ ) ´

(b) (p ^ q´ ) ^ r = (p ^ (q NAND q)) ^ r

• = ((p ^ (NAND q)) NAND r) NAND ((p ^ (q NAND q)) NAND r) = (((p NAND (q NAND q)) NAND (p NAND) (q NAND q))) NAND r) NAND (((p NAND (q NAND q)) NAND (p NAND (q NAND q))) NAND r).

9.6.-El operador del Booleana NOR es definido por p NOR q = (p v q) ´ de v. muestre que {NOR} es un juego completo de operadores.   

 

RESPUESTA:

P´= (p v p) ´ = p NORD p

• p v q = ((p v q )´ )´ = (p NORD q)´ = (p NORD q)  NOR (p NOR q)
• P ^ q = (p´v q´ )´= p´ NOR q´= (p NOR p) NOR (q NOR q)

De, {NOR} is a complete set of operators.

Como una  alternativa, note eso p NAND q = (p ^ q) ´ = ((p´ v q´ ) ´ ) ´ = (p´ NORD q´ )  ´= ((p NOR p) NOR (q NOR q)) ´.

De, p NAND q = ((p NOR p) NOR (q NOR q)) NOR ((p NOR p) NOR (q NOR q)).    

Subsecuentemente NAND  puede expresarse en términos de NOR, y {NAND}  es un juego completo de operadores, {NOR} también es un juego completo de operadores.

 

 

 9.7. - Dibuje un mapa del karnaugh para la expresión del Booleana cuya la forma normal disyuntiva es p´q´r  v  p´qr  v  pqr´  v  pqr y encuentra una versión simplificada de la expresión. 

REPUESTA:

El mapa del karnaugh se muestra en figura

	pq	p´q	p´q´	pq´
r	1	1	1
r´	1

 

Esto contiene dos pares y para que

p´q´r v p´qr v pqr´v pqr = (p´q´r v p´qr) v (pqr´v pqr)

= p´r (q´v q) v pq (r´v r)

= p´r v pq.

 

 

9.8.-Haya la forma normal disyuntiva del f (p, q, r) de función de Booleana con la tabla de verdad mostrada en figura 9.20  

p	q	r	f(p, q, r)
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

 

Dibuje un mapa del karnaugh y  encuentre una versión simplificada de f (p, q, r). 

REPUESTA:

f= p´q´r´ v p´qr´v pq´r v pqr

El mapa del karnaugh

	pq	p´q	p´q´	pq´
r	1			1
r´		1	1

Hay dos pares (uno oculto) 

Simplificando da  p´q´r´ v p´qr´= p´r´ y  pq´r v pqr = pr.

Por consiguiente, f = p´r´v pr.

9.9. - Determine el rendimiento final del circuito de la lógica mostrado en figura 9.21

 

 

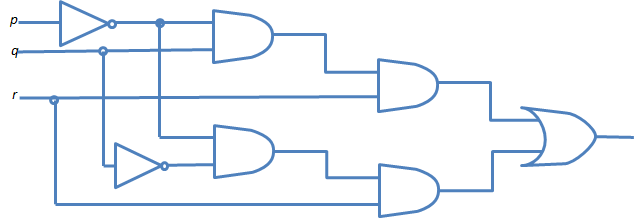
 De, use los karnaugh trazan para encontrar un circuito equivalente que no consiste en uno Y verja uno la verja. 

RESPUESTA:

El rendimiento final es  p´qr v p´q´r  qué tiene el karnaugh trazar como mostrado en figura

	pq	p´q	p´q´	pq´
r		1	1
r´

Simplificando da p´r  y para que el circuito simplificado es como mostrado en la figura

 

 

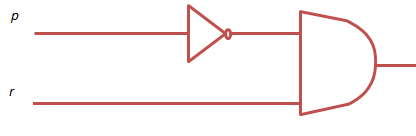
9.10. - Con la ayuda de las leyes de álgebra del Booleana, verifique ese p´ NAND (q´ NAND r) es equivalente a p v (q´ ^ r). 

 

 

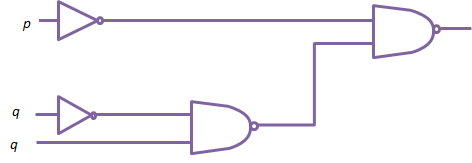
Reemplace el circuito en figura 9.22 con uno equivalente usando uno AND gate, una gate de OR, y un inversor. 

RESPUESTA:

p´ NAND (q´ NAND r) = p´ NAND (q´^ r´ )

= p´ NAND (q v r´ )

= (p´^ (q v r´ ))

= p v (q v r´ ) ´

= p v (q´^ r)

 

 El circuito requerido se muestra en la figura.

 

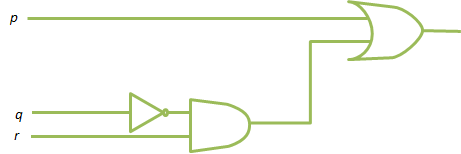
9.11. - la muestra que los dos circuitos de la lógica en figura 9.23 son equivalentes. 

 

 

 

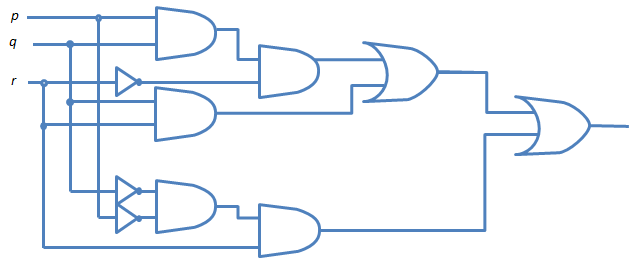
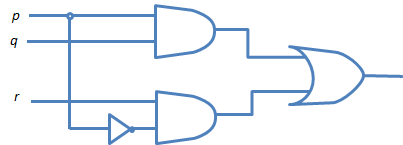
RESPUESTA:

El rendimiento del primer circuito es p´q´r  v  pqr´ v  qr  qué es igual que  p´q´r v pqr´v pqr v p´qr subsecuentemente qr = (p v p´ ) qr.

El rendimiento del segundo circuito es p´r v pq

De la solución a 9.7 anteriormente, p´q´r v pqr´v pqr v p´qr = p´r v pq

De los dos circuitos son equivalentes  

 

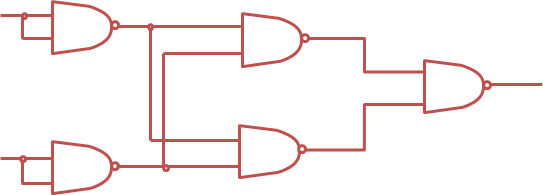
9.12. - Dibuje un circuito de la lógica para la expresión p NOR q que usan Sólo verjas de NAND. [La indirecta: primero verifique ese p NOR q = (p´ NAND q´ ) ´ de NAND y revoca que para cualquier Booleana el r, r´ inconstante = NAND r.]

RESPUESTA:

p NOR q = (p v q) ´ = p´^ q´= ((p´ ^ q´ )´ )´= (p´ NAND q´ )´

= ((p NAND p) NAND (q NAND q)) NAND ((p NAND p) NAND (q NAND q))

El circuito requerido es así como mostrado en la figura

 

 

 

 

 

link del video

www.youtube.com/watch?v=XeDhCTNdXMA