UNIDAD IV
UNIDAD IV
ANALISIS COMBINATORIO
EJERCICIO 6.1
Deseo tomar 2 piezas de frutas para preparar mi almuerzo. Tengo 3 plátanos, 4 manzanas y 2 peras. Cuantas maneras puedo seleccionar con 2 piezas de frutas de diferentes piezas?
SOLUCION
Si selecciona 1 de 3 tres plátanos y 2 de las 4 peras entonces 3 x 4=12, selecciones diferentes podrían ser hechas. Si selecciono 1 plátano y 1 pera habría 3 x 2=6 selecciones diferentes. Finalmente, seleccionando 1 manzana y 1 pera pedo obtener un 4 x 2 =8 maneras diferentes. Como estos 3 juegos de posibilidades son disjuntas, habría 12 + 6 + 8 =26 maneras diferentes de seleccionar 2 piezas de diferentes tipos.
EJERCICIO 6.2
Cuantas licencias distintas de platos están consistiendo de 6 caracteres, el primero de 3 letras y el último de 3 dígitos.
SOLUCION
Cada de 3 letras pueden ser 1 de 26 letras principales del alfabeto. Para la multiplicación principal del número de secuencias diferentes de 3 letras seria 26x26x26=17,756. Similarmente, el numero de secuencias diferentes de 3 dígitos la que pueden aparecer en la licencia de platos es 10x10x10=1000. Finalmente cada licencia de platos de 3 letras seguidas de 3 dígitos, la multiplicación principal seria dando un total de 17, 576,000 platos diferentes.
EJERCICIO 6.3
Una computadora representa integrantes usando el digito binario N, el primer signo indica (+ o -) y restando N-1 representa la magnitud del integrante. Cuantos integrantes distintos pueden ser representados con el digito binario N?
SOLUCION
Cada digito binario es cualquiera como 0 o 1 y tal digito como N. por lo tanto en el numero de binarios diferentes la longitud de la cuerda N es 2N. Diferentes cuerdas binarias corresponden diferentes integrantes excepto para la integración 0 que es representado para 2 cuerdas diferentes: 1 representa + 0 y la otra representa -0. Así puede ser representada 2N -1 diferentes integrantes.
EJERCICIO 6.4
Cuantas palabras de 4 letras pueden ser hechas con las distintas letras de la lista a, g, m, o, p y r?
SOLUCION
Una palabra seleccionada esta ordenada en cualquiera de las diferentes letras para que dé 6 letras. Esto es lo justo.
P (6,4) = 6! = 6!= 6X5X4X3X2X1
(6-2)! 4! 4X3X2X1
Por Anulación:
P (6,4) = 6X5X4X3X2X1 =6X5=30
4X3X2X1
EJERCICIO 6.5
En un restaurante chino usted puede ordenar un menú exactamente de 3 a 7 platos diferentes. Cuantas combinaciones diferentes de 3 platos principales puede ordenar usted?
SOLUCION
Hay
C (7,3)= 7! = 7! = 7X6X5X4X3X2X1
(7-3)!3! 4!3! (4X3X2X1)(3X2X1)
Cancelando da
C (7,3)= = 7X6X5X4X3X2X1
(4X3X2X1)(3X2X1)
= 7X6X5
3X2X1
=35
3 combinaciones diferentes de platos principales
EJERCICIO 6.6
5 dados son arrojados. Cuantos resultados diferentes son posibles?
SOLUCION
Cada dado puede mostrar 1 de 6 resultados. Si 5 dados son arrojados, el numero de resultados son un extra orden seleccionado de 5 objetos con repetición dejando que es C(n+R-1, n-1) con n=6 y R=5. Esto da
C (10,5)= 10!= 252
5!5!
Resultados diferentes.
EJERCICIO 6.7
Doce personas incluyendo a Mary y Perter, son candidatos para servir en un comité de 5. Cuantos comités diferentes son posibles?
De estos cuantos
- Contiene a ambos a Mary y Peter?
- No contiene a ninguno a Mary y Peter?
- Contiene cualquiera de los dos a Mary y Peter?
SOLUCION
Hay
C (12,5)= 12! =792
7!5!
Posibles comités
(a) Si Mary y Peter ya son incluidos nosotros podemos seleccionar 3 miembros más para el comité de 10 personas disponibles. Estos pueden ser determinados en
C (10,3)= 10! =120
7!3!
Por lo tanto, 120 comités contienen a ambos a Mary y Peter
(b) si Mary y Peter son incluidos nosotros podemos seleccionar 5 miembros para el comité de 10 personas disponibles. Estos pueden ser determinados en
C (10,5)= 10! =252
5!5!
Por lo tanto, 252 comités no contienen a Mary ni Peter
(c) Una manera de calcular el número de equipos para formar comités que contenga a Mary, excluyendo a Peter y que contengan a 4 de las otras personas. Estos es justo C (10,4). El mismo número de comités que contenga a Peter y excluya a Mary es 2xC (10,4)=420 comités contiene a cualquiera de los dos a Mary y Peter. Una alternativa aproximada es observar que cada de los 792 comités posibles correspondiente sea preciso a uno de las 3 categorías definidas por (a). (b) y (c). Por lo tanto, el numero requerido en (c) es igual a 792-120-252=420.
MAPA MENTAL
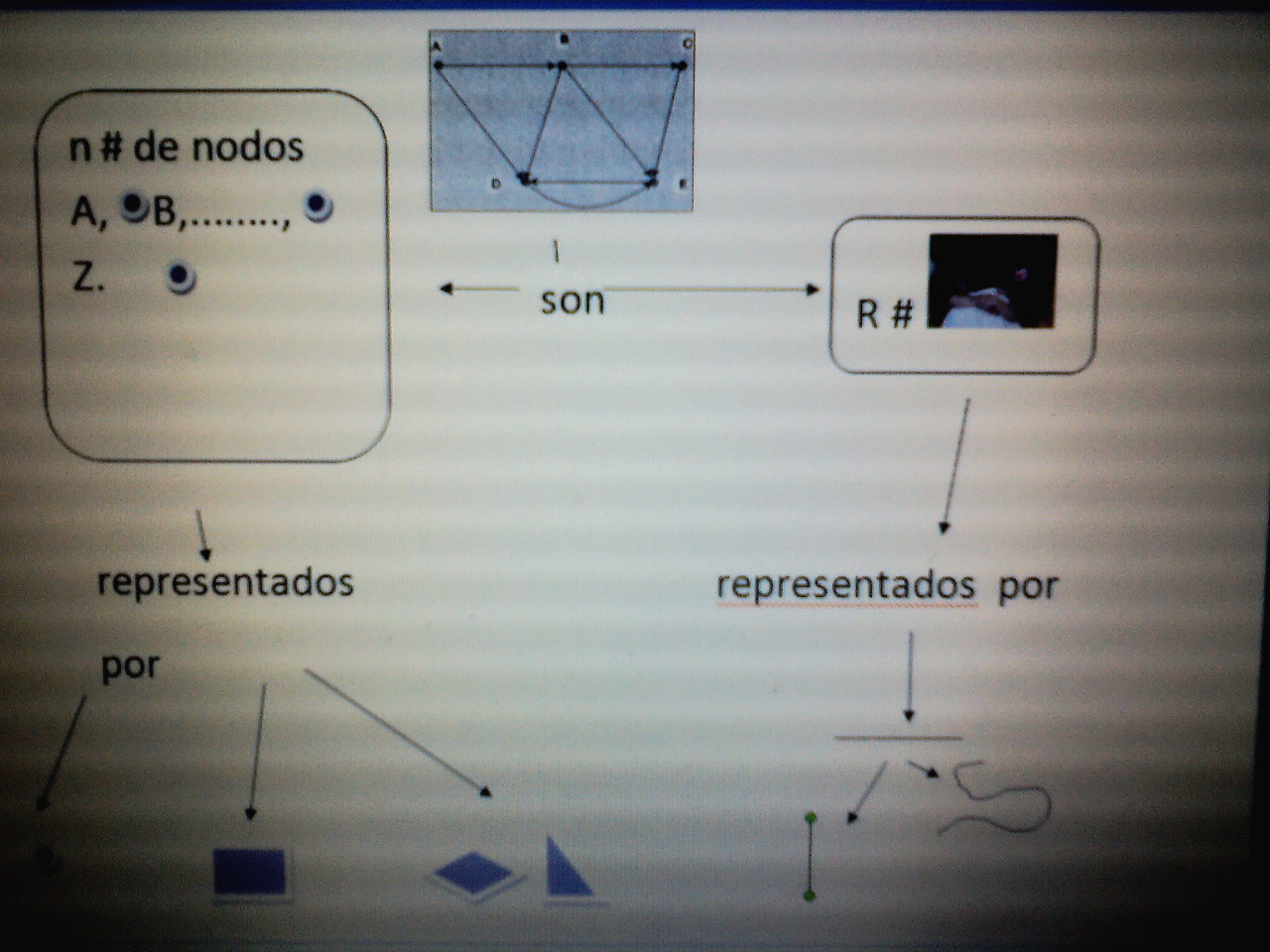
RESUMEN GRAFOS.
los gráfos se originó en el siglo XVIII, cuando el matemático Leonhard Euler, trató de resolver el problema de los puentes de Konigsberg.
En este capítulo se presentan algunas de la terminología estándar utilizada en el estudio de los gráficos y ver una serie de problemas prácticos que se puedan resolver mediante gráfos.
el problema se modela mediante un gráfico que consta de un conjunto de vértices y un conjunto de aristas que conectan estos vértices vertices.the A, B, C y D representan las orillas de los ríos y los bordes a, b, c, d, e, f y g son siete puentes.
un gráfico en el que hay una ruta, comenzando y terminando en el mismo vértice, que utiliza toda la ruta misma se llama un gráfico euleriano.
un gráfico simple se define como un par G = (V, E) donde V es un conjunto finito de vértices y E es un conjunto finito de aristas, de tal manera que G no contiene ciclos (ningún vértice se une a sí mismo por una arista) y no múltiples aristas (nunca hay más de una arista se unió a cualquier par de vértices).
el algoritmo de conectividad.
Sea G = (V, E) un grafo. el algoritmo calcula el valor de c = c (G), el número de componentes conectados de G:
comenzar.
V ': V;
C: = 0;
mientras que V '= 0 hacer
comenzar.
elegir y V E '
encontrar todos los vértices y unidos a por algún camino;
eliminar estos vértices y V'and y de los correspondientes bordes de E;
C: C 1;
final
final
muchos gráficos son hamiltoniano. por ejemplo, si cada vértice en un grafo es adyacente a cada otro vértice siempre hay un ciclo de Hamilton.
las siguientes afirmaciones sobre un grafo G = (V, E) con n vértices y aristas m son equivalentes a la afirmación de que G es un árbol:
hay exactamente un camino entre dos vértices de G.
G está conectado y m = n 1-.
G está conectado y la eliminación de un solo borde desconecta G.
G es acíclico y añadiendo un nuevo borde crea un ciclo.
