link del video

link del video

Buscar en el sitio

Contacto

Blog

video problema 2

Ejemplo 1

Ejemplo 2

UNIDAD IV

unidad III

UNIDAD II

ejecicios unidad 1

video problema 2

UNIDAD V

Ejemplo 1

Ejemplo 2

UNIDAD IV

unidad III

UNIDAD II

ejecicios unidad 1

06.08.2012 00:40

LINK DEL VIDEO DEL PROBLEMA 2

www.youtube.com/watch?v=1MT7frQxezE&feature=plcp

Recurrencia, recursión o recursividad es la forma en la cual se especifica un proceso basado en su propia definición. Siendo un poco más precisos, y para evitar el aparente circuito sin fin en esta definición:

Un problema que pueda ser definido en función de su tamaño, sea este N, pueda ser dividido en instancias más pequeñas (< N) del mismo problema y se conozca la solución explícita a las instancias más simples, lo que se conoce como casos base, se puede aplicar induccion sobre las llamadas más pequeñas y suponer que estas quedan resueltas.

Para que se entienda mejor a continuación se exponen algunos ejemplos:

Factorial(x: Entero): Sea N := x el tamaño del problema, podemos definir el problema de forma recurrente como x*Factorial(x - 1); como el tamaño de Factorial(x - 1) es menor que N podemos aplicar introduccion por lo que disponemos del resultado. El caso base es el Factorial(0) que es 1.

Ordenación por fusión(v: vector): Sea N := tamaño(v), podemos separar el vector en dos mitades. Estas dos mitades tienen tamaño N/2 por lo que por induccion podemos aplicar la ordenación en estos dos subproblemas. Una vez tenemos ambas mitades ordenadas simplemente debemos fusionarlas. El caso base es ordenar un vector de 0 elementos, que está trivialmente ordenado y no hay que hacer nada.

En estos ejemplos podemos observar como un problema se divide en varias (>= 1) instancias del mismo problema, pero de tamaño menor gracias a lo cual se puede aplicar inducción, llegando a un punto donde se conoce el resultado (el caso base)..

Nota: aunque los términos "recursión" y "recursividad" son ampliamente empleados en el campo de la informática, el término correcto en castellano es recurrencia. Sin embargo este último término es algo más específico. Véaserelacion de recurrencia.

Un ejemplo de conjunto definido de forma recurrente es el de losnumeros naturales:

a) 0 pertenece a N

b) Si n pertenece a N, entonces n+1 pertenece a N

c) Si X verifica a) y b) , entonces X está incluido en N

Los números naturales es el conjunto de números enteros no negativos.

INDUCCION MATEMATICA.

de un parámetro $n\,$ que toma una infinidad de valores enteros. En términos simples, la inducción matemática consiste en el siguiente razonamiento:

Premisa mayor: El número entero $a\,$ tiene la propiedad $P\,$ .

Premisa menor: El hecho de que cualquier número entero $n\,$ tenga la propiedad $P\,$ implica que $n+1\,$ también la tiene (que se anota $n \Rightarrow n + 1$ ).

Conclusión: Todos los números enteros a partir de $a\,$ tienen la propiedad $P\,$ .

El razonamiento para demostrar una proposición cualquiera mediante el esquema del razonamiento es como sigue. Llamemos $P_n\,$ a la proposición, donde $n\,$ es el rango.

Se demuestra que $P_0\,$ , el primer valor que cumple la proposición (iniciación de la inducción), es cierta.
Se demuestra que si se asume $P_n\,$ como cierta y como hipótesis inductiva, entonces $P_{n+1}\,$ lo es también, y esto sin condición sobre el entero natural $n\,$ (relación de inducción).

Luego, demostrado esto, concluimos por inducción, que $P_n\,$ es cierto para todo natural $n\,$ .

La inducción puede empezar por otro término que $P_0\,$ , digamos por $P\,$ . Entonces $P_n\,$ será válido a partir del número $n_0\,$ , es decir, para todo natural $n \ge n_0\,$ .

Para todo $n \ge 1$ , $6^n\,$ es un número que acaba en 6.

Sea $P_n\,$ la proposición: « $6^n\,$ acaba en 6».

Es claro que $P_1\,$ es cierto, porque $6^1 = 6\,$ .

Supongamos que $P_n\,$ es cierto para un valor de $n\,$ natural, y probemos $P_{n+1}\,$ .

Un entero acaba por 6 si se puede escribir así: $10a+6\,$ , con $a\,$ entero positivo o igual a cero. La hipótesis es, pues, $6^n=10a+6\,$ .

Entonces $6^{n+1}=6(10a+6)=60a+36=60a+30+6=10(6a+3)+6=10c+6\,$ , con $c=6a+3\,$ , entero.

Esta última escritura prueba que $6^{n+1}\,$ acaba por 6, o sea que $P_{n+1}\,$ es cierto.

Luego $P_n\,$ es cierto para todo $n \ge 1\,$ .

La inducción es válida por la construcción misma del conjunto de los naturales mediante los acciomas de peano. En este caso:

1 es un natural;
si $n\,$ lo es, entonces $n+1\,$ (sucesor de $n\,$ ) lo es también.

Existen otras inducciones, para otros conjuntos elaborados de forma distinta, como por ejemplo la induccion transfinita, y la inducción sobre las fórmulas de la logica propocicional.

Además de la demostracion por induccion, existe la definición o construcción por inducción. Por ejemplo, una sucesión aritmética puede ser definida como función de $n\,$ : $u_n = a + rn\,$ , o por inducción:

$u_0 = a\,$
$u_{n+1} = u_n + r\,$ .

Véase también:sumatorio.

Se tratara de demostrar por inducción la siguiente proposición:

$\sum_{k=1}^n (2k - 1) 3^k = (n - 1) 3^{n+1} + 3$ $\forall n \in \mathbb{N}$

1. Se comprueba para n=1

$\sum_{k=1}^1 (2 - 1) 3^1 = 3 = (1 - 1) 3^{1+1} + 3$

Se tiene por tanto que la proposición es verdadera para n=1

2. Hipótesis inductiva (n=h)

$\sum_{k=1}^h (2k - 1) 3^k = (h - 1) 3^{h+1} + 3$

3. Tesis inductiva (n=h+1)

$\sum_{k=1}^{h+1} (2k - 1) 3^k = (h + 1 - 1) 3^{h+1+1} + 3$

$\sum_{k=1}^{h+1} (2k - 1) 3^k = h 3^{h+2} + 3$

4. Demostración de la tesis con base en la hipótesis

$\sum_{k=1}^{h+1} (2k - 1) 3^k = \sum_{k=1}^{h} (2k - 1) 3^k +(2(h+1) - 1) 3^{h+1}$

Se aplica la hipótesis de inducción:

$\sum_{k=1}^{h+1} (2k - 1) 3^k = (h - 1) 3^{h+1} + 3 + [2(h+1) - 1] 3^{h+1}$

$\sum_{k=1}^{h+1} (2k - 1) 3^k = (h - 1) 3^{h+1} + 3 + (2h+2 - 1) 3^{h+1}$

$\sum_{k=1}^{h+1} (2k - 1) 3^k = 3^{h+1} (h - 1 + 2h + 1) + 3$ (sacando factor común)

$\sum_{k=1}^{h+1} (2k - 1) 3^k = 3^{h+1} 3h + 3$

$\sum_{k=1}^{h+1} (2k - 1) 3^k = h 3^{h+2} + 3$

Por lo tanto, por verificarse la proposición para n=1 y para n=k+1 siendo k cualquier número natural, la proposición se verifica $\forall n \in \mathbb {N}$

29.07.2012 21:17

UNIDAD IV

ANALISIS COMBINATORIO

EJERCICIO 6.1

Deseo tomar 2 piezas de frutas para preparar mi almuerzo. Tengo 3 plátanos, 4 manzanas y 2 peras. Cuantas maneras puedo seleccionar con 2 piezas de frutas de diferentes piezas?

SOLUCION

Si selecciona 1 de 3 tres plátanos y 2 de las 4 peras entonces 3 x 4=12, selecciones diferentes podrían ser hechas. Si selecciono 1 plátano y 1 pera habría 3 x 2=6 selecciones diferentes. Finalmente, seleccionando 1 manzana y 1 pera pedo obtener un 4 x 2 =8 maneras diferentes. Como estos 3 juegos de posibilidades son disjuntas, habría 12 + 6 + 8 =26 maneras diferentes de seleccionar 2 piezas de diferentes tipos.

EJERCICIO 6.2

Cuantas licencias distintas de platos están consistiendo de 6 caracteres, el primero de 3 letras y el último de 3 dígitos.

SOLUCION

Cada de 3 letras pueden ser 1 de 26 letras principales del alfabeto. Para la multiplicación principal del número de secuencias diferentes de 3 letras seria 26x26x26=17,756. Similarmente, el numero de secuencias diferentes de 3 dígitos la que pueden aparecer en la licencia de platos es 10x10x10=1000. Finalmente cada licencia de platos de 3 letras seguidas de 3 dígitos, la multiplicación principal seria dando un total de 17, 576,000 platos diferentes.

EJERCICIO 6.3

Una computadora representa integrantes usando el digito binario N, el primer signo indica (+ o -) y restando N-1 representa la magnitud del integrante. Cuantos integrantes distintos pueden ser representados con el digito binario N?

SOLUCION

Cada digito binario es cualquiera como 0 o 1 y tal digito como N. por lo tanto en el numero de binarios diferentes la longitud de la cuerda N es 2^N. Diferentes cuerdas binarias corresponden diferentes integrantes excepto para la integración 0 que es representado para 2 cuerdas diferentes: 1 representa + 0 y la otra representa -0. Así puede ser representada 2^N -1 diferentes integrantes.

EJERCICIO 6.4

Cuantas palabras de 4 letras pueden ser hechas con las distintas letras de la lista a, g, m, o, p y r?

SOLUCION

Una palabra seleccionada esta ordenada en cualquiera de las diferentes letras para que dé 6 letras. Esto es lo justo.

P (6,4) = 6! = 6!= 6X5X4X3X2X1

(6-2)! 4! 4X3X2X1

Por Anulación:

P (6,4) = 6X5X4X3X2X1 =6X5=30

4X3X2X1

EJERCICIO 6.5

En un restaurante chino usted puede ordenar un menú exactamente de 3 a 7 platos diferentes. Cuantas combinaciones diferentes de 3 platos principales puede ordenar usted?

SOLUCION

Hay

C (7,3)= 7! = 7! = 7X6X5X4X3X2X1

(7-3)!3! 4!3! (4X3X2X1)(3X2X1)

Cancelando da

C (7,3)= = 7X6X5X4X3X2X1

(4X3X2X1)(3X2X1)

= 7X6X5

3X2X1

=35

3 combinaciones diferentes de platos principales

EJERCICIO 6.6

5 dados son arrojados. Cuantos resultados diferentes son posibles?

SOLUCION

Cada dado puede mostrar 1 de 6 resultados. Si 5 dados son arrojados, el numero de resultados son un extra orden seleccionado de 5 objetos con repetición dejando que es C(n+R-1, n-1) con n=6 y R=5. Esto da

C (10,5)= 10!= 252

5!5!

Resultados diferentes.

EJERCICIO 6.7

Doce personas incluyendo a Mary y Perter, son candidatos para servir en un comité de 5. Cuantos comités diferentes son posibles?

De estos cuantos

Contiene a ambos a Mary y Peter?
No contiene a ninguno a Mary y Peter?
Contiene cualquiera de los dos a Mary y Peter?

SOLUCION

Hay

C (12,5)= 12! =792

7!5!

Posibles comités

(a) Si Mary y Peter ya son incluidos nosotros podemos seleccionar 3 miembros más para el comité de 10 personas disponibles. Estos pueden ser determinados en

C (10,3)= 10! =120

7!3!

Por lo tanto, 120 comités contienen a ambos a Mary y Peter

(b) si Mary y Peter son incluidos nosotros podemos seleccionar 5 miembros para el comité de 10 personas disponibles. Estos pueden ser determinados en

C (10,5)= 10! =252

5!5!

Por lo tanto, 252 comités no contienen a Mary ni Peter

(c) Una manera de calcular el número de equipos para formar comités que contenga a Mary, excluyendo a Peter y que contengan a 4 de las otras personas. Estos es justo C (10,4). El mismo número de comités que contenga a Peter y excluya a Mary es 2xC (10,4)=420 comités contiene a cualquiera de los dos a Mary y Peter. Una alternativa aproximada es observar que cada de los 792 comités posibles correspondiente sea preciso a uno de las 3 categorías definidas por (a). (b) y (c). Por lo tanto, el numero requerido en (c) es igual a 792-120-252=420.

MAPA MENTAL

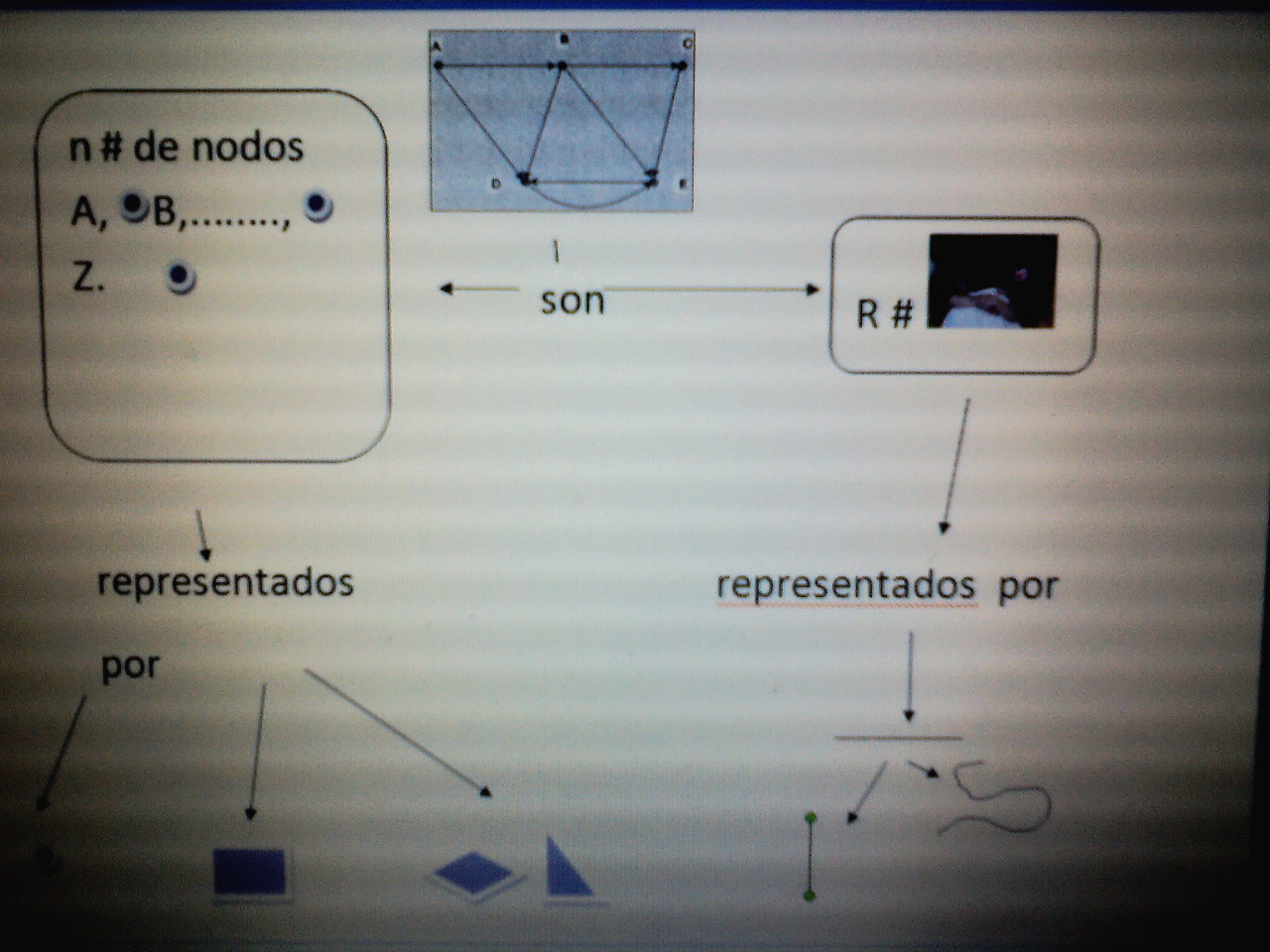
RESUMEN GRAFOS.

los gráfos se originó en el siglo XVIII, cuando el matemático Leonhard Euler, trató de resolver el problema de los puentes de Konigsberg.

En este capítulo se presentan algunas de la terminología estándar utilizada en el estudio de los gráficos y ver una serie de problemas prácticos que se puedan resolver mediante gráfos.

el problema se modela mediante un gráfico que consta de un conjunto de vértices y un conjunto de aristas que conectan estos vértices vertices.the A, B, C y D representan las orillas de los ríos y los bordes a, b, c, d, e, f y g son siete puentes.

un gráfico en el que hay una ruta, comenzando y terminando en el mismo vértice, que utiliza toda la ruta misma se llama un gráfico euleriano.

un gráfico simple se define como un par G = (V, E) donde V es un conjunto finito de vértices y E es un conjunto finito de aristas, de tal manera que G no contiene ciclos (ningún vértice se une a sí mismo por una arista) y no múltiples aristas (nunca hay más de una arista se unió a cualquier par de vértices).

el algoritmo de conectividad.
Sea G = (V, E) un grafo. el algoritmo calcula el valor de c = c (G), el número de componentes conectados de G:
comenzar.
V ': V;
C: = 0;
mientras que V '= 0 hacer
comenzar.
elegir y V E '
encontrar todos los vértices y unidos a por algún camino;
eliminar estos vértices y V'and y de los correspondientes bordes de E;
C: C 1;

final
final

muchos gráficos son hamiltoniano. por ejemplo, si cada vértice en un grafo es adyacente a cada otro vértice siempre hay un ciclo de Hamilton.

las siguientes afirmaciones sobre un grafo G = (V, E) con n vértices y aristas m son equivalentes a la afirmación de que G es un árbol:

hay exactamente un camino entre dos vértices de G.
G está conectado y m = n 1-.
G está conectado y la eliminación de un solo borde desconecta G.
G es acíclico y añadiendo un nuevo borde crea un ciclo.

29.07.2012 21:16

UNIDAD 3

RELACIONES Y GRAFOS

EJERCICIO 4.1

Considerando las tres familias dado en la figura 4.1

Fred y Mavis John y Mary

Alice Ken y Sue Mike Penny

Jane Fiona Alan

Figura 4.1

Escribe abajo el orden de las parejas correspondientes de la siguiente relación en la serie P de las personas de estas tres familias.

(a) R = {(x, y): x es un abuelo de y}

(b) S= {(x, y): x es una hermana de y}

SOLUCION

(a) R contenido del orden de las parejas:

(Fred, Jane),(Fred,Fiona),(Fred,Alan),(John,Jane),(John,Fiona) y (John,Alan).

(b) S contenido del orden de las parejas:

(Sue,Penny),(Penny,Sue),(Jane,Fiona), (Fiona,Jane ), (Alice,Ken),(Sue,Mike), (Penny,Mike),(Jane,Alan) y (Fiona,Alan).

EJERCICIO 4.2

Escribe el orden de las parejas correspondientes de las siguientes relaciones binarias entre A= {1, 3, 5, 7} y B= {2, 4, 6}:

(a) U = {(x, y): x + y = 9}

(b) V = {(x, y): x < y}

SOLUCIÓN

(a) U contenido del orden de las parejas (3,6), (5,4) y (7,2).

(b) V contenido del orden de las parejas (1,2), (1,4), (1,6), (3,4), (3,6) y (5,6).

EJERCICIO 4.3

De la siguiente relación definida en A= {1, 2, 3, 4, 5,6}:

R= {(x, y): x es un divisor de y}

Escribe abajo el orden de las parejas correspondientes de R.

SOLUCION

R contenido de parejas:

(1,1),(1,2),(1,3),(1,4),(1,5)(1,6),(2,2),(2,4),(2,6),(3,3),(3,6),(4,4),(5,5) y (6,6).

EJERCICIO 4.4

Hallar la relación de la dirección en la representación grafica de R en el ejemplo 4.3.

SOLUCION

Entonces la relación de las parejas de R es. {1, 2, 3, 4, 5,6} y la dirección de la grafica tiene seis vértices. Dado el diagrama correspondiente que está en la figura 4.3.

La relación de las parejas son los números y las vértices el total de las flechas.

EJERCICIO 4.5

La relación R en las parejas de A= {a, b, c,d) tiene la siguiente representación matriz donde las filas y las columnas deben de poner el nombre de los elementos de A en el orden dado.

F T T F

F F T T

F T F F

T T F T

Enlista el orden de las parejas correspondientes de R.

SOLUCION

La relación de la constante R es el orden de las parejas (a,b), (a,c),(b,c),(b,d),(c,b),(d,a),(d,b) y (d,d).

EXAMEN

01.07.2012 15:18

9.1. - Use tablas de verdad para establecer de las leyes del Morgan’s.

Las tablas de verdad requeridas aparecen a continuación. Desde los valores en el examen final dos columnas son idénticas que las mesas verifican eso Del Morgan´s leyes sostenimiento.

9.2. - Con la ayuda de las leyes de álgebra del booleana verifique a lo siguiente:

(a) (p ˄ q´ ) ´ v r´= p´ v q v r´

(b) ((p ˄ q´ ) ˄ (r v (p ˄ q´ ))) ´ = p´v q

RESPUESTA:

(a) (p ˄ q´ ) ´ v r´= p´ v q v r´ = (p´ v q) v r´= p´ v q v r´ Usando De las leyes de Morgan´s, las leyes asociativas y (q´ ) ´= q.

(b) ((p ˄ q´ ) ˄ (r v (p ˄ q´ ))) ´ =

=(p ˄ q´ ) v (r v (p ˄ q´ )) ´ por las leyes de Morgan´s
=(p´ v q) v (r´^ (p ˄ q´ )´ ) por las leyes de Morgan´s y el hecho que (q´ )´=q
=(p´v q) v (r´^(p´v q)) por las leyes de Morgan´s
= ((p´v q) v r´ ) ^ (p´v q) por el distributivo y leyes de impotencia.
= p´v q por la absorción y leyes de impotencia.

9.3. - El hallazgo la forma normal disyuntiva del g = g (p, q, r, s) de función de Booleana) con la tabla de verdad mostrada en figura 9,19.

p	q	r	s	g
0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

RESPUESTA:

p´q´r´s v p´q´rs´ v pq´rs v pqr´s

9.4.- Estructura la tabla de verdad para la expresión Booleana (p ^ (q ´ v r)) v (p´ ^ (q v r´ )) y determina su forma normal disyuntiva.

RESPUESTA:

Permita f = (p ^ (q´ v r)) v (p´ ^ (q v r´ )). La Tabla de verdad para f se da en figura s9.2

p	q	r	q´ v r	q v r´	p^(q´ v r)	p´^(q v r´ )	f
0	0	0	1	1	0	1	1
0	0	1	1	0	0	0	0
0	1	0	0	1	0	1	1
0	1	1	1	1	0	1	1
1	0	0	1	1	1	0	1
1	0	1	1	0	1	0	1
1	1	0	0	1	0	0	0
1	1	1	1	1	1	0	1

La forma normal disyuntiva es:

p´q´r´ v p´qr´ v p´qr v pq´r´ v pq´r v pqr

9.5. - Escriba la expresión (p ^ el q´ ) ^ r

(a) usando a sólo los operadores v y ´,

(b) usando a sólo los operadores NAND.

RESPUESTA:

(a) (p ^ q´ ) ^ r = (((p ^ q´ ) ^ r) ´ ) ´= ((p ^ q´ ) ´ v r´ ) = ((p´v q) v r´ ) ´= (p´v q v r´ ) ´

(b) (p ^ q´ ) ^ r = (p ^ (q NAND q)) ^ r

= ((p ^ (NAND q)) NAND r) NAND ((p ^ (q NAND q)) NAND r) = (((p NAND (q NAND q)) NAND (p NAND) (q NAND q))) NAND r) NAND (((p NAND (q NAND q)) NAND (p NAND (q NAND q))) NAND r).

9.6.-El operador del Booleana NOR es definido por p NOR q = (p v q) ´ de v. muestre que {NOR} es un juego completo de operadores.

RESPUESTA:

P´= (p v p) ´ = p NORD p

p v q = ((p v q )´ )´ = (p NORD q)´ = (p NORD q) NOR (p NOR q)
P ^ q = (p´v q´ )´= p´ NOR q´= (p NOR p) NOR (q NOR q)

De, {NOR} is a complete set of operators.

Como una alternativa, note eso p NAND q = (p ^ q) ´ = ((p´ v q´ ) ´ ) ´ = (p´ NORD q´ ) ´= ((p NOR p) NOR (q NOR q)) ´.

De, p NAND q = ((p NOR p) NOR (q NOR q)) NOR ((p NOR p) NOR (q NOR q)).

Subsecuentemente NAND puede expresarse en términos de NOR, y {NAND} es un juego completo de operadores, {NOR} también es un juego completo de operadores.

9.7. - Dibuje un mapa del karnaugh para la expresión del Booleana cuya la forma normal disyuntiva es p´q´r v p´qr v pqr´ v pqr y encuentra una versión simplificada de la expresión.

REPUESTA:

El mapa del karnaugh se muestra en figura

	pq	p´q	p´q´	pq´
r	1	1	1
r´	1

Esto contiene dos pares y para que

p´q´r v p´qr v pqr´v pqr = (p´q´r v p´qr) v (pqr´v pqr)

= p´r (q´v q) v pq (r´v r)

= p´r v pq.

9.8.-Haya la forma normal disyuntiva del f (p, q, r) de función de Booleana con la tabla de verdad mostrada en figura 9.20

p	q	r	f(p, q, r)
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

Dibuje un mapa del karnaugh y encuentre una versión simplificada de f (p, q, r).

REPUESTA:

f= p´q´r´ v p´qr´v pq´r v pqr

El mapa del karnaugh

	pq	p´q	p´q´	pq´
r	1			1
r´		1	1

Hay dos pares (uno oculto)

Simplificando da p´q´r´ v p´qr´= p´r´ y pq´r v pqr = pr.

Por consiguiente, f = p´r´v pr.

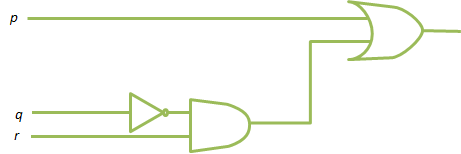
9.9. - Determine el rendimiento final del circuito de la lógica mostrado en figura 9.21

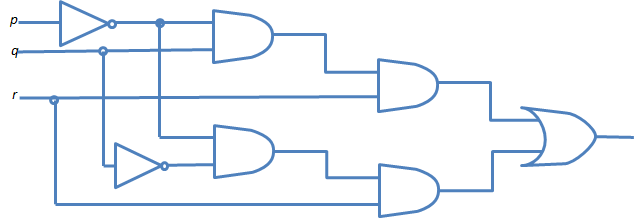
De, use los karnaugh trazan para encontrar un circuito equivalente que no consiste en uno Y verja uno la verja.

RESPUESTA:

El rendimiento final es p´qr v p´q´r qué tiene el karnaugh trazar como mostrado en figura

	pq	p´q	p´q´	pq´
r		1	1
r´

Simplificando da p´r y para que el circuito simplificado es como mostrado en la figura

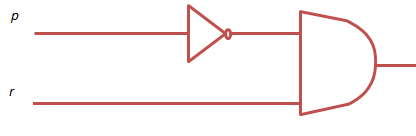
9.10. - Con la ayuda de las leyes de álgebra del Booleana, verifique ese p´ NAND (q´ NAND r) es equivalente a p v (q´ ^ r).

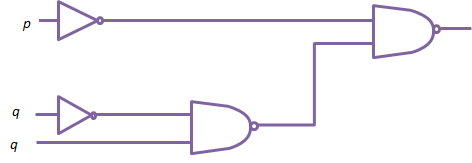
Reemplace el circuito en figura 9.22 con uno equivalente usando uno AND gate, una gate de OR, y un inversor.

RESPUESTA:

p´ NAND (q´ NAND r) = p´ NAND (q´^ r´ )

= p´ NAND (q v r´ )

= (p´^ (q v r´ ))

= p v (q v r´ ) ´

= p v (q´^ r)

El circuito requerido se muestra en la figura.

9.11. - la muestra que los dos circuitos de la lógica en figura 9.23 son equivalentes.

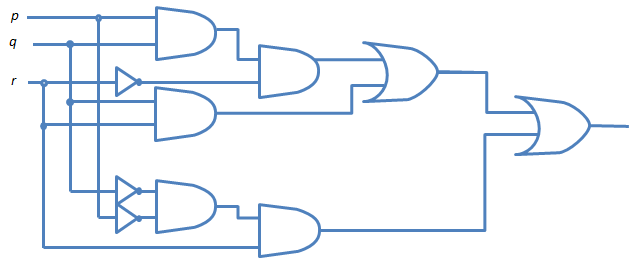
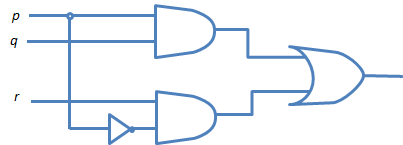
RESPUESTA:

El rendimiento del primer circuito es p´q´r v pqr´ v qr qué es igual que p´q´r v pqr´v pqr v p´qr subsecuentemente qr = (p v p´ ) qr.

El rendimiento del segundo circuito es p´r v pq

De la solución a 9.7 anteriormente, p´q´r v pqr´v pqr v p´qr = p´r v pq

De los dos circuitos son equivalentes

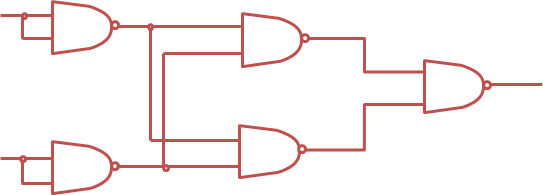
9.12. - Dibuje un circuito de la lógica para la expresión p NOR q que usan Sólo verjas de NAND. [La indirecta: primero verifique ese p NOR q = (p´ NAND q´ ) ´ de NAND y revoca que para cualquier Booleana el r, r´ inconstante = NAND r.]

RESPUESTA:

p NOR q = (p v q) ´ = p´^ q´= ((p´ ^ q´ )´ )´= (p´ NAND q´ )´

= ((p NAND p) NAND (q NAND q)) NAND ((p NAND p) NAND (q NAND q))

El circuito requerido es así como mostrado en la figura

www.youtube.com/watch?v=XeDhCTNdXMA

25.06.2012 22:20

ejercicio 1 expresa con codigo binario los numeros decimales sig.

a) 47

47/2=23 +1

23/2=11+

11/2=5+1

5/2=2+1

2/2=1+0

1/2=0+1

b) 191= 10111111

191/2=95+1

95/2=47+1

47/2=23+1

23/2=11+1

11/2=5+1

5/2=2+1

2/2=1+0

1/2=0+1

c) 25= 11001

25/2=12+1

12/2=6+0

6/2=3+0

3/2=1+1

1/2=0+1

d)99= 1100011

99/2=49+1

49/2=24+1

24/2=12+0

12/2=6+0

6/2=3+0

3/2=1+1

1/2=0+1

e) 67=1000011

67/2=33+1

33/2=16+1

16/2=8+0

8/2=4+0

4/2=2+0

2/2=1+0

1/2=0+1

f)135= 10000111

135/2=67+1

67/2=33+1

33/2=16+1

16/2=8+0

8/2=4+0

4/2=2+0

2/2=1+0

1/2=0+1

g) 276= 100010100

276/2=138+0

138/2=69+0

69/2=34+1

34/2=17+0

17/2=8+1

8/2=4+0

4/2=2+0

2/2=1+0

1/2=0+1

2.- expresa el sustema decimal los sig. numeros binarios

a) 110111 b) 111000

=1*2^5+1*2^4+0*2^3+1*2^2+1*2^1+1*2^0 =1*2^5+1*2^4+1*2^3+0*2^2+0*2^1+0*2^0

=32+16+0+4+2+1 =32+16+8+0+0+0

=55 =56

c) 010101 d) 101010

=0*2^5+1*2^4+0*2^3+1*2^2+0*2^1+1*2^0 =1*2^5+0*2^4+1*2^3+0*2^2+1*2^1+0*2^0

=0+16+0+4+0+1 =32+0+8+0+2+0

=21 =42

e) 1111110

=1*2^6+1*2^5+1*2^4+1*2^3+1*2^2+1*2^1+0*2^0

=64+32+16+8+4+2+0

=126

3.-dados dos numeros binarios 01001000 y 0100010 ¿cual de ellos es el mayor?¿podras compararlos sin necesidad de convertirlos a sistema decimal?

4.-si y es el 01001000 ya que el segundo 1 esta mas serca un lugar ala izquierda que el segundo 1 del segundo numero binario

¿cuantos numeros diferentes se pueden escribir utilizando el sistema binario de numeracion con solo 3 digitos?¿y con 16?

en 3= a 8 numeros diferentes

en 16= a 65536 numeros diferentes

5.- convierte los sig numeros octales a decimales

a) 45 b)125

=4*8^1+5*8^0 =1*8^2+2*8^1+5*8^0

=32+5 =64+16+5

=37 =85

c)625

=6*8^2+2*8^1+5*8^0

=384+16+5

=405

6.-convierte los siguientes numeros decimales en octales.

a) 63 b)513 c)119

63/8=7+7 513/8=64+1 119/8=14+7

7/8=0+7 64/8=8+0 14/8= 1+6

= 77 8/8= 1+0 1/8=0+1

1/8=0+1 = 167

=1001

7,-convierte los siguientes números binarios a octales.

a)1101101 b)101110

001 101 101 =0*2^2+0*2^1+1*2^0

=0*2^2+0*2^1+1*2^0 =4+0+1=5

=0+0+1=1 =1*2^2+1*2^1+0*2^0

=1*2^2+0*2^1+1*2^0 =4+2+0=6

=4+0+1=5 =56

=155

c) 11011011 d)101101011

011 011 011 =1*2^2+0*2^1+1*2^0

=0*2^2+1*2^1+1*2^0 =4+0+1 = 5

=0+2+1= 3 = 0*2^2+1*2^1+1*2^0

=0*2^2+1*2^1+1*2^0 =0+2+1=3

=0+2+1=3 = 553

=333

8,-convierte los siguientes números s octales a binario.

a) 25 b)372

25/2=12+1 372/2=186+ 0

12/2= 6+0 186/2= 93+0

6/2= 3+0 93/2= 46+1

3/2=1+1 46/2=23+ 0

1/2=0+1 23/2=11+1

=11001 11/2=5+1

5/2=2+1

2/2=1+0

½= 0+1

=101110100

c) 2753

2753/2=1376+1

1376/2=688+0

688/2=344+0

344/2=172+0

172/2=86+0

86/2=43+0

43/2=21+1

21/2=10+1

10/2=5+0

5/2=2+1

2/2=1+0

½=0+1

=101011000001

9.- realiza a siguiente suma de números binarios

a)111011 + 110 = 1000001

b) 111110111 + 111001 = 1000110000

c) 10111+11011+10111= 1001001

10:-realiza la suma de números octales

365+ 23= 410

=3*8^2+6*8^1+5*8^0

=192+48+5=245

2*8^1+3*8^0

= 16+3=19

245+19= 264

264/8=33+0

33/8=4+1

4/8= 0+4

= 410

11:- suma los siguientes numeros hexadecimales.

a) 17A + 3C

17A= 1*16ᶺ2+7*16ᶺ1+A*16ᶺ0= 256+112+0

=378

3C= 3*16ᶺ1+C*16ᶺ0= 48+12

=60

378+60= 438

438/16=27+6

27/16= 1+11

1/16=0+1

= 1B6

b) 20F5+31B

20F5= 2*16ᶺ3+0*16ᶺ2+15*16ᶺ1+5*16ᶺ0= 8192+0+240+5

=8437

31B=3*16ᶺ2+1*16ᶺ1+11*16ᶺ0= 786+16+11

=795

8437+795=9232

9232/16=577+0

577/16=36+1

36/16= 2+4

4/16=0+4

=4410

c)2E70C+1AA7F

2E70C=2*16ᶺ4+14*16ᶺ3+7*16ᶺ2+0*16ᶺ1+12*16ᶺ0=131072+57344+1792+0+12

=190220

1AA7F=1*16ᶺ4+10*16ᶺ3+10*16ᶺ2+7*16ᶺ1+15*16ᶺ0=65536+40960+2560+112+15

=109183

190220+109183=299403

299403/16=18712+11

18712/16=1169+8

1169/16=73+1

73/16=4+9

4/16=0+4

=4918B

12.- realiza las siguientes restas de numeros binarios

a) 11011-110=110101

b) 111110111-111001=110111110

c) 1010111-11011-10011=101011

13.-resta los siguientes numeros octales

a) 365-23=336

365= 3*8ᶺ2+6*8ᶺ1+5*8ᶺ0=192+48+5=241

23=2*8ᶺ1+3*8ᶺ0=16+3=19

241-19=222

222/8=27+6

27/8=3+3

3/8=0+3

b)2732-1265

2732=2*8ᶺ3+7*8ᶺ2+3*8ᶺ1+2*8ᶺ0=1024+448+24+2=1498

1265=1*8ᶺ3+2*8ᶺ2+6*8ᶺ1+5*8ᶺ0=512+128+5=693

1498-693=805

805/8=100+5

100/8=12+4

12/8=1+4

1/8=0+1

=1445

14.- realiza las siguientes restas de números hexadecimales

a) 17A – 3C

(17 A) (3C) (318)

=1*16^2+ 7*16^1+ 10*16^0 =3*16^1+12*16^0 318/16=19+4

1/16= 0+1

(13E)

=1*125+7*16+10 =3*16+12*1 19/16=1+3

=256+112+10 =48+12

=378 =60

378-60=318

b) 20F5+31B

20F5= 2*16ᶺ3+0*16ᶺ2+15*16ᶺ1+5*16ᶺ0= 8192+0+240+5

=8437

31B=3*16ᶺ2+1*16ᶺ1+11*16ᶺ0= 786+16+11

=795

8437-795=7642

7642/16=477+10

477/16=29+13

29/16= 1+13

1/16=0+1

=1DDA

c)2E70C+1AA7F

2E70C=2*16ᶺ4+14*16ᶺ3+7*16ᶺ2+0*16ᶺ1+12*16ᶺ0=131072+57344+1792+0+12

=190220

1AA7F=1*16ᶺ4+10*16ᶺ3+10*16ᶺ2+7*16ᶺ1+15*16ᶺ0=65536+40960+2560+112+15

=109183

190220-109183=80437

80437/16=5027+5

5027/16=314+3

314/16=19+10

19/16=1+3

1/16=0+1

=13A35

p´ ^ q´

(p v q)´

p	q	r	s	g
0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

p	q	r	s	g
0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

p	q	r	s	g
0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0